Applying Over-Sampling Methods to Highly Imbalanced Data

I mentioned various undersampling approaches for dealing with highly imbalanced data in the earlier post “Applying Under-Sampling Methods to Highly Imbalanced Data” In this article, I present oversampling strategies for dealing with the same problem.

By reproducing minority class examples, oversampling raises the weight of the minority class. Although it does not provide information, it introduces the issue of over-fitting, which causes the model to be overly specific. It is possible that while the accuracy for the training set is great, the performance for unseen datasets is poor.

Oversampling Methods

1. Random Oversampling of the minority class

Random oversampling just replicates the minority class instances at random. Overfitting is thought to be more likely when random oversampling is used. Random undersampling, on the other hand, has the main disadvantage of discarding useful data.

2. Synthetic Minority Oversampling Technique (SMOTE)

Chawla et al. (2002) present the Synthetic Minority Over-sampling Technique to avoid the over-fitting problem (SMOTE). This approach, which is regarded state-of-the-art, is effective in many different applications. Based on feature space similarities between existing minority occurrences, this approach produces synthetic data. To generate a synthetic instance, it locates the K-nearest neighbours of each minority instance, chooses one at random, and then performs linear interpolations to generate a new minority instance in the neighbourhood.

3. ADASYN: Adaptive Synthetic Sampling

Motivated by SMOTE, He et al. (2009) introduce and garner widespread attention for the Adaptive Synthetic sampling (ADASYN) approach.

ADASYN creates minority class samples based on their density distributions. More synthetic data is generated for minority class samples that are more difficult to learn than for minority class samples that are easier to learn. It computes each minority instance’s K-nearest neighbours, then uses the class ratio of the minority and majority examples to produce new samples. Repeating this method adaptively adjusts the decision boundary to focus on difficult-to-learn instances.

Application with Python

The three oversampling strategies are demonstrated below. The code can be found on my github page.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

from imblearn.over_sampling import (RandomOverSampler, 
                                    SMOTE, 
                                    ADASYN)
# RandomOverSampler
  # With over-sampling methods, the number of samples in a class
  # should be greater or equal to the original number of samples.
sampler = RandomOverSampler(sampling_strategy={1: 2590, 0: 300})
X_rs, y_rs = sampler.fit_resample(X_train, y_train)
print(f'RandomOverSampler {Counter(y_rs)}')
plot_data(X_rs,y_rs, 'Random Oversampling')

# SMOTE
sampler = SMOTE(sampling_strategy={1: 2590, 0: 300})
X_rs, y_rs = sampler.fit_resample(X_train, y_train)
print(f'SMOTE {Counter(y_rs)}')
plot_data(X_rs,y_rs,'SMOTE')

# ADASYN
sampler = ADASYN(sampling_strategy={1: 2590, 0: 300})
X_rs, y_rs = sampler.fit_resample(X_train, y_train)
print(f'ADASYN {Counter(y_rs)}')
plot_data(X_rs,y_rs)

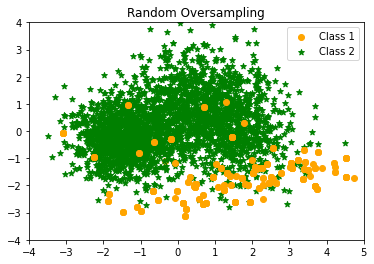
RandomOverSampler Counter({1: 2590, 0: 300})

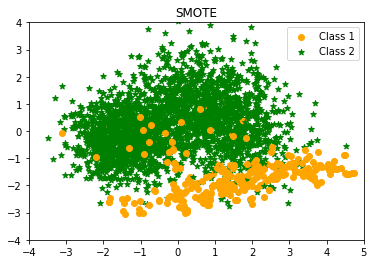
SMOTE Counter({1: 2590, 0: 300})

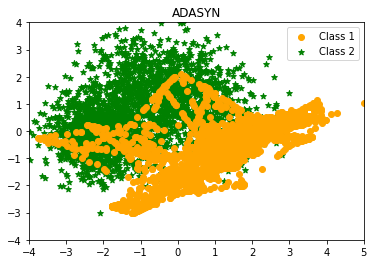
ADASYN Counter({0: 2604, 1: 2589})

The previous article Applying Under-Sampling Methods to Highly Imbalanced Data along with this article together can give you a comprehensive view of both the undersampling and oversampling techniques!

Conclusion

I hope this post has helped you better grasp this subject. Thank you very much for reading! 😄